Framework
A probability only makes sense if it is reliable. This article explains how to verify that a “60%” actually corresponds to an observed frequency close to 60%, and why this is central to any serious analysis.
Accuracy ≠ calibration
Accuracy measures the number of correct predictions. Calibration measures the statistical honesty of probabilities. A model can be accurate but poorly calibrated, or the opposite.
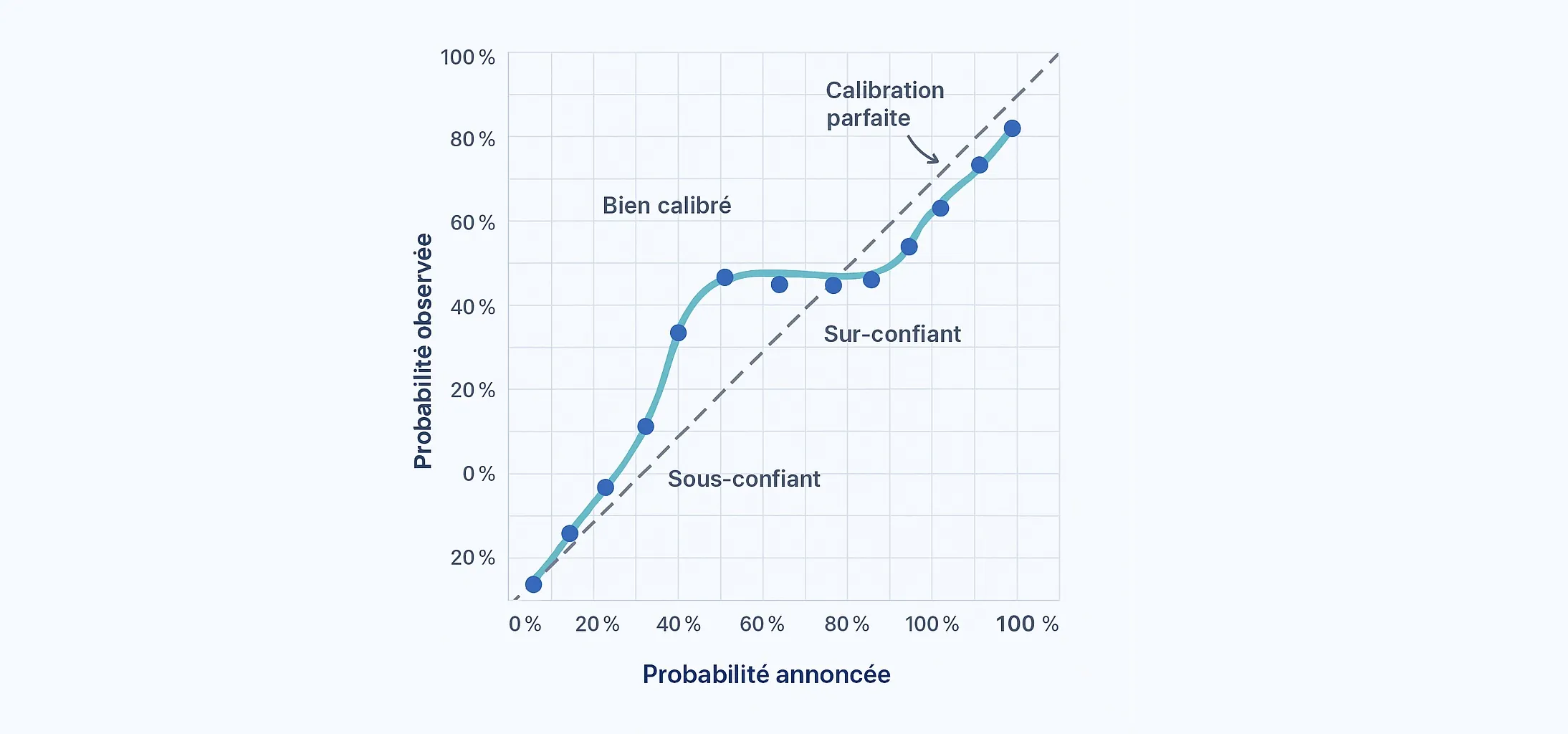
- Well calibrated: 70% announced → ~70% observed
- Overconfident: 70% → ~63% observed
- Underconfident: 70% → ~76% observed
Reliability metrics
Brier Score
The Brier Score measures the squared error between probability and actual outcome. It heavily penalizes unjustified certainty.
LogLoss
LogLoss is particularly sensitive to highly confident mistakes. It is useful for detecting overconfidence.
Reliability curve
Probabilities are grouped into bins and compared to observed frequencies. The diagonal represents perfect calibration.
Why calibration must be tracked over time
Leagues evolve, styles change, refereeing evolves as well. Without regular recalibration, a model can remain “good” while gradually becoming misleading.
This logic is detailed in the algorithm journal .
How to read a probability properly
- a probability is an expected frequency, not a promise
- calibration matters more than the raw value
- thresholds are always a volume / stability trade-off
Conclusion
A probability is only useful if it is reliable. Calibration turns a percentage into actionable information, by making uncertainty readable rather than misleading.